Różnorodność produkowanego asortymentu przez przedsiębiorstwa na całym świecie wymaga optymalizacji jego podatności transportowej. Powstające wyroby docierając w najodleglejsze zakamarki globu przemierzają długą drogę. Są  poddawane wewnętrznym czynnościom przeładunkowym oraz magazynowym. Transportowane zewnętrznymi środkami, takimi jak różnorodne samochody dostawcze, statki czy samoloty. Podlegają wielu czynnością manipulacyjnym – załadunki, rozładunki itp. – nim dotrą do docelowego odbiorcy.

A stamtąd nierzadko wiedzie jeszcze podobna droga do ostatecznego konsumenta – indywidualnego odbiorcy, który powinien otrzymać towar najwyższej klasy, bez jakichkolwiek uszkodzeń.

I tutaj z pomocą przychodzą opakowania, które nie tylko ze względu na swoje właściwości ochronią produkt. Współczesne technologie oraz różnorodność surowców, a zwłaszcza szeroka paleta tektur falistych umożliwia indywidualne dopasowanie wymiarów do potrzeb całego cyklu transportowego i magazynowego. Często tworzone są ładunki zbiorcze – czyli łączone są drobne wyroby, pojedyncze opakowania w większą całość. Albo też dzielone duże ładunki na mniejsze partie. Opakowania kartonowe są nieodzownym elementem takich operacji.

W każdym przedsiębiorstwie widoczne są regały zapełnione towarem w pudłach wykonanych z tektury falistej. Jednak same regały mają określone parametry wymiarowe. Tak samo jak różnorodność stosowanych środków transportowych, maszyn pakujących, urządzeń ładunkowych, dróg itp. Wymaga określonych gabarytów przewożonego towaru. W tym celu podjęte zostały prace normalizacyjne nad ujednoliceniem systemów wymiarowych.

Normalizacja opakowań

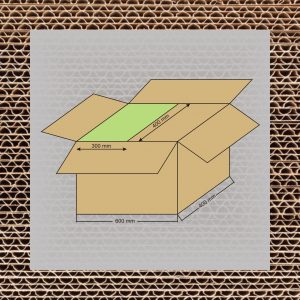
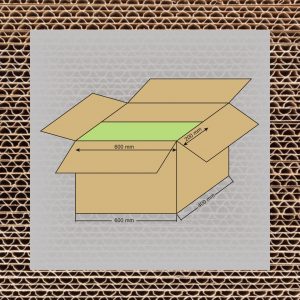
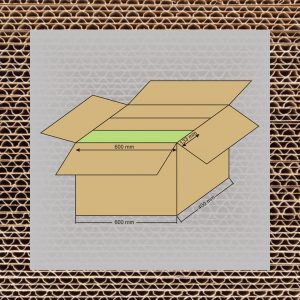
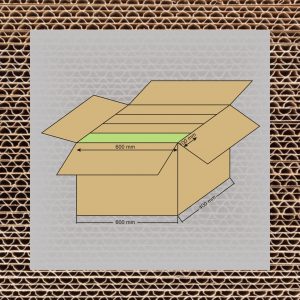
W rezultacie tych działań opracowana została norma ISO 3394-1974 (E) „Dimension of rigid rectangular packages – transport packages”. Jej zapisy wprowadziły do międzynarodowego obrotu towarowego typoszereg wymiarowy ładunków jednostkowych. Oparty on został na podstawowym module powierzchni podstawy opakowania 400mm x 600mm.

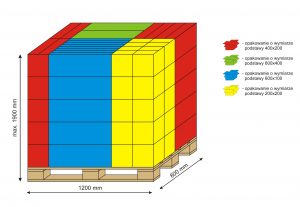
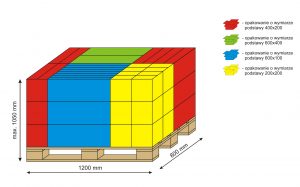
Jak widać jest on idealnie dostosowany do palety o wymiarach 800mmx1200mm oraz do palety, której wymiary wynoszą1000mmx1200mm. Poprzez mnożenie albo dzielenie podstawowego wymiaru modułu (400mm i 600mm) można otrzymać cały system opakowań modułowych.

Opakowania modułowe – typoszereg

Dokładnie odzwierciedla to samą definicję modułu, w myśl której przez moduł rozumie się umowną jednostkę miary. Odpowiada ona wielkości określonego elementu, a jej zadaniem jest wyznaczenie proporcji oraz wzajemnych zależności wszystkich elementów całości.

 

 

 

 

 

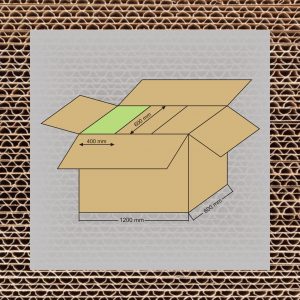
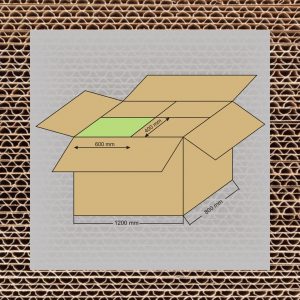
Logiczną konsekwencją jest wskazanie 5-ciu multimodułów – będących wielokrotnością modułu podstawowego, tj.:

1. 1200 x 1000
2. 1200 x 800
3. 1200 x 600
4. 1200 x 400
5. 800 x  600

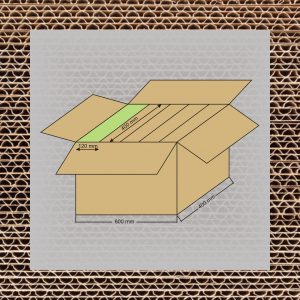
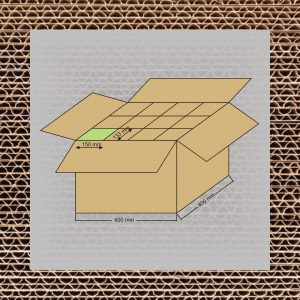
Oraz 19-tu submodułów – będących całkowitą podwielokrotnością podstawy 600mm x 400mm, tj.:

1. 600 x 200
2. 600 x 133
3. 600 x 100
4. 300 x 400
5. 300 x 200
6. 300 x 133
7. 300 x 100
8. 200 x 400
9. 200 x 200
10. 200 x 133
11. 200 x 100
12. 150 x 400
13. 150 x 200
14. 150 x 133
15. 150 x 100
16. 120 x 400
17. 120 x 200
18. 120 x 133
19. 120 x 100

Ograniczenia i ich konsekwencje

Opracowanie wymiarów powierzchni podstawy jest jednak czynnikiem, który nie wyczerpuje w pełni tematu związanego z optymalnym wykorzystaniem całej przestrzeni magazynowej czy transportowej. Istotna jest tutaj również wysokość opakowania. Wysokość ładunków wymagała także ujednolicenia.

 

 

Przyjęto standardy, które uwzględniają jedne z ważniejszych kryteriów, tj.:

1. Wielkość otworów drzwiowych, doków, bram, skrzyń samochodów dostawczych oraz przestrzeni ładunkowej kontenerów, pojemników itp. W całym łańcuchu transportowym
2. Wysokość regałów magazynowych
3. Wysokość pomieszczeń – hal produkcyjnych, magazynów, placówek handlowych
4. Wymiary drzwi dźwigów oraz urządzeń podnośnikowych
5. Wysokość podnoszenia urządzeń służących do transportu drogowego

Wysokość załadunku – czyli wysokość ładunku + wysokość palety według ustanowionych standardów wynosi:

1. 105 cm
2. 160 – 190 cm.

Ostatecznym decydentem jest producent, który w porozumieniu ze swoimi odbiorcami decyduje według jakich standardów będą pakowane jego produkty. W każdym jednak przypadku wszelkie działania zmierzają do utworzenia tzw. „skrzyni logistycznej”. Jest ona typowym przykładem modułowego systemu opakowań. Taka forma opakowania transportowego umożliwia płynność całego procesu transportowego, kompatybilnego ze współczesną techniką.

Proporcje mają swoją historię

Warto wspomnieć, że struktury modułowe są schematem powielonym w dużej mierze ze świata sztuki. Autor „Czterech ksiąg o architekturze.” – Andree Palladia podzielił średnicę podstawy kolumny na 60 minut i przyjął 30 minut jako moduł służący do określenia proporcji innych elementów danej całości. Bowiem idealnie wyważone proporcje stwarzają wrażenie ładu i harmonii. Aby je uzyskać artyści już w starożytności kierowali się intelektem, obliczając je matematycznie. Popularne były poglądy wywodzące się z filozoficznej szkoły pitagorejczyków. Rozpowszechniali oni pogląd, że ład i harmonia są układami ilościowymi. Zależą zatem od miary, liczby i proporcji. W konsekwencji piękno jest przedmiotem obliczeń matematycznych. Podziwiając plastyczne dzieła Greków możemy być pewni, że w większości powstały one w wyniku obliczeń matematycznych.

I kto by przypuszczał w tych tak odległych czasach, że zostanie to przeniesione na grunt współczesnej logistyki. W której niezwykle istotnym elementem jest również ład, harmonia, porządek. A patrząc na paletę z opakowaniami modułowymi trudno zaprzeczyć zachowaniu proporcji.

Źródła:

• „Logistyczne systemy transportu bliskiego i magazynowania.” – Zbigniew Korzeń
• „Systemy logistyczne.” – Hans-Christian Pfohl
• „Sztuka i czas. Od prehistorii do rokoka.” – Barbara Osińska